How the Spectra of Stars Arise

To create an extremely simple model of a star we take a solid sphere surrounded by a layer of gaseous material. The sphere should be hot enough to emit visible light. The spectrum of this glowing sphere is smooth and does not show any absorption features. The gaseous layer adds some absorption line and maybe some lines in emission to our stellar model.

The Radiation of a Black Body

At first we focus in the solid sphere at a high temperature. We take a halogen or tungsten lamp^wp as that supposed solid base of the star. Varying the electric current we get different temperatures of the filament and the emitted light looks not only brighter at higher temperatures but has also a slightly different hue. The white balance of the camera used was in fixed mode during these shots.

Apparently the brightness of the lamp changes with power and so does the color of the emitted light. There is a pysical model handling this case of a dense material at different temperatures. This model is is called the Black Body^wp.

The luminosity of a Black Body is ruled by the Stefan-Boltzmann law ^wp \[L_{\mathrm{bol}}=\sigma A T^4\] where \(L_{\mathrm{bol}}\) is the bolometric luminosity of the body, \(A\) ist surface area and \(T\) its temperature. The working temperature of a halogen lamp at the designed power is around 3000 K. We calculate from the formula above 1000 K and 2010 K using the electrical power as \(L_{\mathrm{bol}}\).

The hue of the emitted light depends on the shape of the spectrum in the visible region. Especially at wich wavelength the spectrum peaks. We get this wave length with Wien's displacement law ^wp. \[\lambda_{\mathrm{peak}}=\frac{b}{T}\] where \(b \approx 2.898\cdot10^{-3}\,\mathrm{mK}\) is called Wien's displacement constant. Obviously the most prominent wave length \(\lambda_{\mathrm{peak}}\) decreases with increasing temperature. The color changes from red, orange, yellow, white, bluish to blue while the temperature increases.

With the help of astropy and matplotlib we can easily calculate and demonstrate spectra of black bodys with the temperatures of our cool rsp. hot star.

The ordinate of the two spectra is in kilo watts per square meter, solid angle and bandwidth of only 1 Ångstrom. In our very simplified stellar model these lines represent the stellar continuum.

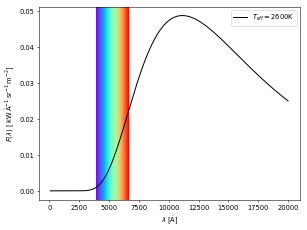
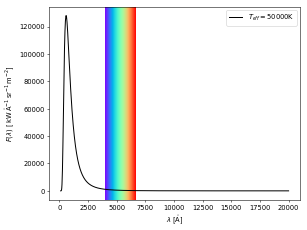
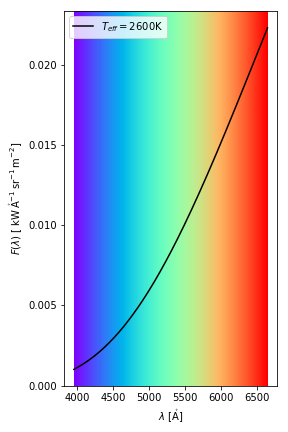
We see more clearly the reason for the stellar colors if we compare only the visible part of the two spectra.

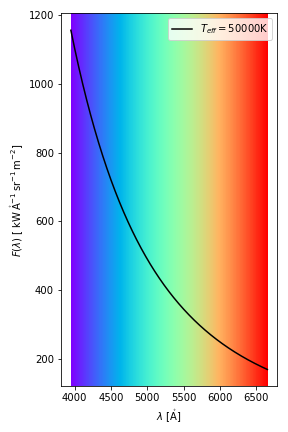
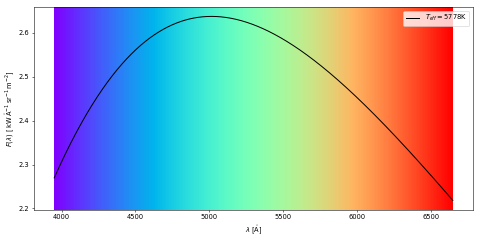
And now a spectrum of a black body at 5778 K, i.e. our Sun.