Resolving Power
The resolution of a spectrum at wavelength \(\lambda\) is \[R = R_{\lambda} = \frac{\lambda}{\Delta\lambda}\] We take \(R_{\lambda}\) because the resolution may change with the wavelength under consideration. \(\Delta\lambda\) is the smallest difference in wavelength at which two spectral lines can still be perceived separately. This is the same problem as with the perception of binary stars. There are therefore different definitions for \(\Delta\lambda\). We use the FWHM definition here and are aware that this is a fairly rough criterion. But it is in common use.
A long-slit spectrograph does not image a single spectral line as a uniformly bright stripe with a rectangular brightness curve, but rather as a curve with more or less broadly sloping edges. The width of this brightness function at half height is FWHM, full width at half maximum. Since the brightness curve is approximately Gaussian, the software used for wavelength calibration usually fits a Gaussian function to the spectral line.
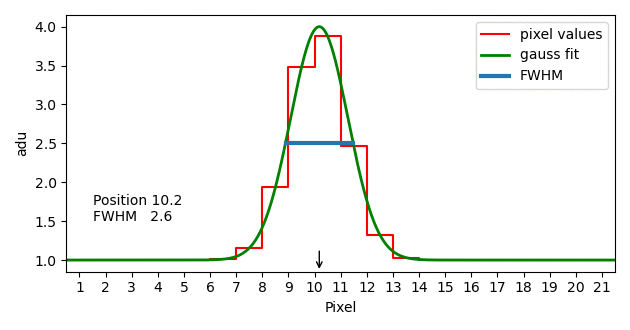
If the reduced object spectrum still contains the telluric lines, the resolution can be obtained from the width of unblended telluric lines at half the depth. If you determine the resolution in both ways, you get slightly different values. This is due to the different lighting of the entrance slit. I therefore always round the resolution to two valid digits.
More about the benefits of tellurics in Tellurics and in Errors.
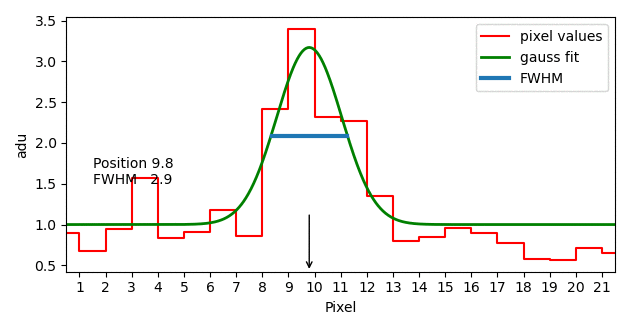
The values change a bit if you add 25% noise. In this extreme example is \(S\!N\!R=4\).
Last modified: 2023 Nov 25