Measuring the Noise
No matter what you do, the spectrum always contains at least stellar flux and noise. To estimate the quality of the measured flux, the ratio of signal to noise is determined. \[S\!N\!R = \frac{flux}{noise}\] There are two ways to measure noise relative to the signal.
If you know the number of electrons \(n_e\) in the pixels, then the root of the average number of electrons is, to a fairly good approximation, the value of the SNR. \[S\!N\!R = \sqrt{n_e}\]
However, the software used often normalizes the measured spectrum to values close to 1. Then you look for an area of the spectrum that is not too small and does not contain any features such as emission lines or absorption lines, normalize it and determine the standard deviation in the normalized section.
We use an approximately 200px large section, fit a third degree polynomial to the shape of the flux and divide this flux by the fit. The result now contains a constant star signal of amplitude 1 and the noise that is always present. We take the standard deviation \(\sigma\)of the small standardized section as the noise amplitude. \[S\!N\!R = \frac{1}{\sigma}\]
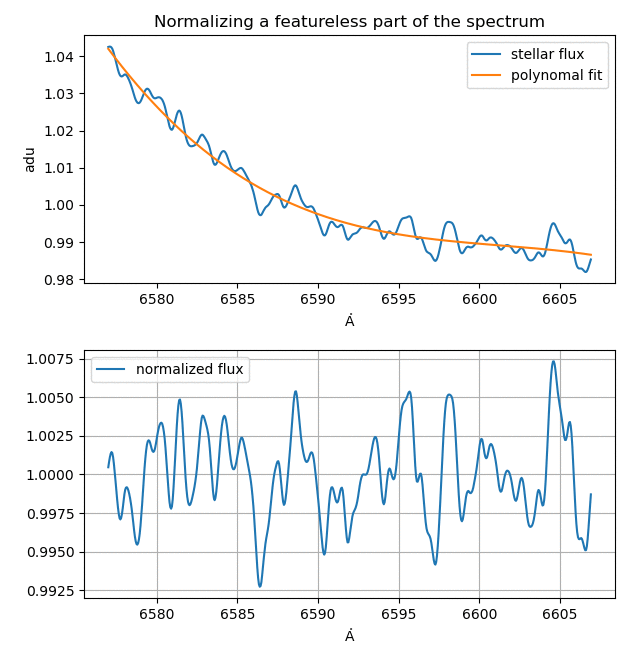
The SNR will be used later to estimate errors. We save it in the header of the file.
Last modified: 2023 Nov 25